Suunto PM-5 Manuale utente

La pagina si sta caricando...

Suunto PM-5, PM-5/1520

GUIDE DE L'UTILISATEUR

FR

La pagina si sta caricando...

Suunto PM-5, PM-5/1520

GUÍA DEL USUARIO

ES

La pagina si sta caricando...

Suunto PM-5, PM-5/1520

GUIDA DELL'UTENTE

IT

La pagina si sta caricando...

4

PM-5/1520

METRO OTTICO PER ALTEZZA

Il metro per altezza Suunto PM-5/1520 è uno strumento per misurare le altezze, in

particolare quelle degli alberi, con grande precisione e velocità. Lo strumento è in

lega di alluminio anodizzato anticorrosione. La scheda della scala scorre su un

supporto speciale all'interno di un contenitore di plastica sigillato ermeticamente e

riempito con un liquido che ne consente lo scorrimento libero e l'arresto rapido. Il

liquido non gela, conserva inalterate le proprietà umettanti durante il suo utilizzo ed

elimina le fastidiose vibrazioni della scala.

ISTRUZIONI PER L'USO

Se misurate da distanze di 15 m e 20 m, le altezze degli alberi possono essere lette

direttamente dalle scale dello strumento. Le letture devono essere raddoppiate

durante la misurazione da distanze di 30 m e 40 m. Il metro per altezza Suunto può

essere utilizzato anche per determinare l'angolo di un gradiente. Ciò viene realizzato

eseguendo un puntamento lungo la linea del gradiente, utilizzando la scala di 20 m

alla sinistra dello strumento. La lettura così ottenuta può essere controllata nella

tabella di conversione sul retro dello strumento per ottenere l'angolo.

5

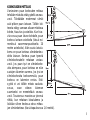
MISURAZIONE DELL'ALTEZZA

La misurazione effettiva dell'altezza di

un albero deve essere effettuata dalla

distanza misurata come segue:

l'osservatore individua la cima

dell'albero tenendo entrambi gli occhi

ben aperti. Una volta avvistato

l'oggetto, la linea di puntamento e la

scala saranno simultaneamente

visibili nel campo visivo dello

strumento. Appena la linea di

puntamento coincide con la cima

dell'albero l'altezza potrà essere letta

(in questo esempio, da una scala di

20 m alla sinistra dello strumento). La

lettura ottenuta è l'altezza dell'albero

misurata dall'altezza degli occhi

dell'osservatore. La base dell'albero

deve essere ancora individuata. Se è

situata sotto l'altezza degli occhi

dell'osservatore allora l'altezza

effettiva dell'albero viene ottenuta

sommando le due letture. Se è al di

sopra dell'altezza degli occhi dell'osservatore l'altezza dell'albero viene ottenuta

sottraendo la differenza tra le due letture. In realtà, nell'ultimo caso la distanza non

può essere misurata in orizzontale. Pertanto, per ottenere un risultato corretto con la

6

massima precisione, attenersi alla seguente procedura. Al livello del suolo le letture

della cima dell'albero sono solitamente sufficienti: è necessario aggiungere

semplicemente l'altezza del livello degli occhi dell'osservatore (1,60 m in questo

caso) che è già nota.

ISTRUZIONI PER L'USO DEL

NOMOGRAMMA

Se a causa di un terreno irregolare la

distanza non può essere determinata

orizzontalmente come nella procedura

sopracitata utilizzare il nomogramma di

pagina 7.

STABILIRE LA DISTANZA BASE

Dato che questo strumento non è dotato di prisma, la distanza base di (ad esempio)

15 m deve essere determinata utilizzando un metro a nastro lungo il terreno.

Aggiungere o sottrarre le letture dalla cima e dalla base per determinare l'altezza

apparente. Sul nomogramma di pagina 7, posizionare l'altezza apparente sulla scala

a destra. Sulla scala doppia a sinistra individuare la lettura ottenuta dall'avvistamento

della base dell'albero. Le letture per gradienti di salita o di discesa devono essere

effettuate da lati differenti della scala. Collegare questi due punti del nomogramma

con una linea retta. Adesso la scala centrale del nomogramma indica la reale altezza

dell'albero.

7

Nota importante

Gli assi visivi di alcune persone non sono

paralleli, tale disturbo è detto eteroforia.

Può variare nel tempo e dipendere da

diversi fattori. Pertanto, per assicurarsi

che tale fenomeno non si ripercuota sulla

precisione delle letture, si consiglia

all'utente di controllare tale eventualità

prima di effettuare letture, utilizzando la

seguente procedura: eseguire una lettura

tenendo entrambi gli occhi aperti, quindi

chiudere quello libero. Se la lettura non

cambia notevolmente, gli assi visivi sono

allineati ed è possibile tenere entrambi gli

occhi aperti. Se dovesse verificarsi una

differenza nelle letture, tenere l'altro

occhio aperto e fissare lo strumento a

mezza altezza. In tal modo si creerà

un'illusione ottica, dove la linea di

puntamento prosegue oltre il corpo dello

strumento e viene visualizzata

sull'obiettivo.

In salita

Lettura alla base

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

21

20

19

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

2

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

m

Altezza apparente

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

m

Altezza corretta

L-20

m

In pendenza

8

PM-5

CLINOMETRO A LETTURA OTTICA

La struttura robusta e le dimensioni ridotte rendono il

CLINOMETRO SUUNTO la soluzione ideale per ogni

tipo di lavoro. Facile per una lettura rapida grazie alla

lente priva di parallasse incorporata nel design.

L'avvistamento e la lettura della scala vengono eseguiti

simultaneamente. Non vi sono viti da girare, bolle da

centrare o da regolare.

Quando lo spazio è limitato, come nelle operazioni

geologiche e mineralogiche, l'inclinazione degli strati e

di altre formazioni può essere letta posizionando lo

strumento lungo la linea o la superficie della

formazione, leggendo l'angolo direttamente dalla

finestra laterale.

Caratteristiche della struttura

La struttura è in alluminio leggero anticorrosione.

La scheda della scala è sostenuta da un gruppo di

supporto in pietra dura e tutte le parti mobili sono

immerse in un liquido di smorzamento all'interno di un

resistente contenitore di plastica sigillato

ermeticamente. Il liquido smorza tutte le vibrazioni di scala eccessive e consente un

movimento fluido privo di scosse della scheda della scala.

Il materiale del contenitore resiste alla luce solare e all'acqua. Il liquido non si congela

in presenza di basse temperature, né evapora in caso di alte temperature.

Scala

percentuale

positiva e

negativa

Scala di

gradi positivi

e negativi

Reticolo

ampliato da

illusione

ottica

Scala di gradi

addizionale nella

finestra laterale

9

Specifiche

Peso: 120 g/119,07 g Dimensioni: 74 x 52 x 15 mm / 2 3/4" x 2" x 5/8". Le scale

ottiche sono graduate in gradi da 0° a +/-90° e da 0 % a +/-150%.

Sul retro dello strumento è stampata una tabella di coseni.

Risoluzione

Esegue direttamente letture fino a un minimo di un grado o dell'uno per cento. Può

eseguire una stima fino a 10 minuti o 1/5 dell'1 percento, l'ultima misura è ovviamente

valida per le letture intorno al livello dello zero.

VERSIONI DI PM-5 DISPONIBILI

Il PM-5/360 PC di base è stato modificato adeguandolo a combinazioni di scala

diverse per utilizzi speciali. Pertanto, è disponibile una versione con ”grado nuovo” o

scala granulometrica. Invece della normale divisione in 360 gradi la divisione

completa del cerchio è di 400 gradi (g). La scala percentuale è normale. Il modello è

PM-5/400 PC.

10

ISTRUZIONI PER L'USO

Le letture vengono solitamente eseguite con l'occhio destro. A causa delle differenze

nell'acutezza visiva e delle preferenze personali, a volte è più facile utilizzare l'occhio

sinistro. È di importanza fondamentale che entrambi gli occhi siano ben aperti. La

mano di sostegno non deve ostruire la visibilità dell'altro occhio.

Lo strumento viene posto davanti all'occhio di lettura, in modo da poter leggere la

scala tramite l'oculare mentre la finestra circolare è rivolta a sinistra. Lo strumento

viene puntato verso l'oggetto sollevandolo o abbassandolo, finché la linea di

puntamento non viene visualizzata sul punto da misurare. Al tempo stesso la

posizione della linea di puntamento rispetto alla scala fornisce la lettura corretta. A

causa di un'illusione ottica, la linea di puntamento (reticolo) sembra proseguire fuori

dell'alloggiamento e pertanto può essere osservata sul terreno o sull'oggetto.

La scala di sinistra indica l'angolo di inclinazione in gradi dal piano orizzontale

all'altezza degli occhi. La scala di destra indica l'altezza del punto di avvistamento

dalla stessa altezza degli occhi orizzontale ed è espressa nella percentuale della

distanza orizzontale. Il seguente esempio ne illustra la procedura:

11

L'obiettivo è misurare l'altezza

di un albero da una distanza di

25 m/82 piedi sopra il livello

del suolo. Lo strumento è

inclinato in modo da

visualizzare la linea di

puntamento sulla cima

dell'albero (apice). La lettura

ottenuta sarà pari al 48

percento (circa 25,5°). Dato

che la distanza è di 25 m/82

piedi, l'altezza dell'albero è 48/

100 x 25 m = circa 12 m oppure

48/100 x 25 m = ca. 12 m

oppure 48/100 x 82 piedi =

circa 39 piedi. A tale risultato è

necessario aggiungere l'altezza

dell'occhio dal suolo, ovvero

1,6’ m o 5 ½ piedi. La somma è

13,6’ m o 44 ½ piedi, quindi

l'altezza dell'albero.

Per misurazioni estremamente precise, soprattutto su terreni in pendenza, è

necessario effettuare due letture: una per la cima e l'altra per la base del tronco.

Quando la base del tronco è posta al di sotto dell'altezza degli occhi, le percentuali

ottenute vengono sommate. L'altezza totale è la percentuale di somma della distanza

orizzontale. Ad esempio, se la lettura dell'apice è 41 % e la lettura al terreno è 13 %,

12

l'altezza totale dell'albero misurata da una distanza di 25 m/82 piedi è di (41 + 13)/

100 x 25 m = 54/100 x 25 m = circa 13.513,5 m oppure in piedi (41 + 13)/100 x 82

piedi = 54/100 x 82 piedi = circa 44 ½ piedi.

Quando la base del tronco è al di sopra dell'altezza degli occhi la lettura della base

viene sottratta dalla lettura dell'apice e l'altezza totale equivale alla percentuale di

differenza della distanza orizzontale.

Ad esempio, se la lettura dell'apice è 65 % e la lettura della base è 14 %, l'altezza

totale è (64 - 14)/100 x 25 m = 50/100 x 25 m = 12,5 m oppure in piedi (64 - 14)/100

x 82 piedi = 50/100 x 82 piedi = 41 piedi. Quando i calcoli vengono eseguiti

mentalmente, si consiglia di utilizzare una distanza di misurazione di 50, 100 o 200

m/piedi per semplificare l'operazione.

13

Tutte le letture della scala percentuale sono basate sulla distanza orizzontale. Ciò

significa che se la distanza sul terreno in pendenza viene misurata lungo il terreno si

verificherà un errore che deve essere corretto per ottenere dei risultati precisi. Nella

maggioranza dei casi l'errore risulta insignificante per gli angoli di inclinazione del

terreno di dimensioni ridotte, ma aumenta progressivamente con l'incremento

dell'angolo.

La correlazione trigonometrica è

H = h x cos

α

Dove H sta per l'altezza effettiva o corretta, h è l'altezza osservata e α (alfa) è

l'angolo di inclinazione del terreno. Utilizzando tale equazione è possibile correggere

anche la distanza. In tal caso h sta per la distanza misurata lungo il terreno e H è la

distanza orizzontale. Se viene utilizzata la distanza giusta non è necessario

correggere l'altezza osservata. Durante il calcolo della distanza orizzontale

utilizzando la distanza del terreno e l'inclinazione si potrebbe verificare un errore

qualora l'inclinazione venisse misurata dall'altezza degli occhi alla base del tronco. La

misurazione dell'inclinazione sul terreno potrebbe risultare scomoda. Per evitare

errori, misurare l'angolo di inclinazione dall'altezza degli occhi fino al punto di

avvistamento eseguito o posizionato sul tronco all'altezza degli occhi; così facendo le

due linee di misurazione diventano parallele. Il vero angolo dell'inclinazione è di 9

gradi.

14

L'esempio mostrato nell'immagine seguente illustra entrambi i metodi di calcolo.

Metodo 1. Misurazione della distanza del terreno. Questa è di 25 m/82 piedi. Quindi

misurare l'angolo di inclinazione. L'angolo è di 9 gradi. Leggere le percentuali dei

punti della cima e del terreno. Sono 20 e 23 percento.

Calcolo:

Prendere il 52 percento di 25 m/82 piedi, che è 13 m/42,6 piedi e moltiplicarlo per il

coseno di 9 gradi.

0,987 x 13 m = 12,8 m oppure in piedi 0,987 x 42,6 piedi = 42 piedi.

Metodo 2. Moltiplicazione della distanza del terreno per il coseno dell'angolo di

inclinazione.

0,987 x 25 m = 24,6 m oppure in piedi 0,987 x 82 piedi = 80,9 piedi.

23

100

-------- -

29

100

-------- -

52

100

-------- -=+

15

Come nella procedura precedente, aggiungere le letture in percentuale e prendere la

somma percentuale della distanza corretta.

oppure in piedi

Questo esempio mostra che un angolo di inclinazione di 9 gradi causa una

correzione di solo 2,3 percento, ma quando l'angolo di inclinazione è di 35 gradi, la

correzione comporta una riduzione di circa il 18 percento dell'altezza osservata.

52

100

-------- -

24 6m 12 8m,=,×

52

100

-------- -

80 9ft 42ft=,×

16

CORREZIONE NOMOGRAFICA DELL'ALTEZZA

Utilizzando il nomogramma tutte le correzioni del calcolo si rivelano inutili. Per

ottenere la soluzione nomografica è necessario solo un righello o un altro oggetto

dotato di un bordo rettilineo. Per utilizzare il nomogramma, posizionare il righello in

modo che il bordo intersechi la scala dell'angolo a sinistra sul punto di inclinazione

dell'angolo e la scala dell'altezza osservata (a destra) sul punto corretto. L'altezza (o

distanza) corretta viene letta nel punto dove il bordo interseca il centro della scala

dell'altezza corretta. Utilizzando una distanza di misurazione di 100 m/piedi lungo il

terreno la procedura di correzione diventa assai semplice. A quel punto non è

necessaria alcuna misurazione dell'angolo di inclinazione. È sufficiente solo la lettura

del punto superiore e del punto inferiore. In base alla situazione, la loro somma o

differenza dà come risultato l'altezza apparente direttamente in piedi. Tale risultato

può essere corretto nel modo seguente: prima di tutto, nella scala di destra del

nomogramma trovare il punto che indica l'altezza apparente. Quindi, nella scala

doppia di sinistra del nomografo trovare il punto che indica la lettura del punto del

terreno. A questo punto collegare tali punti. La lettura corretta verrà rilevata dalla

relativa scala di mezzo in corrispondenza del punto di intersezione. In questa

procedura l'angolo di inclinazione può essere ignorato, poiché la scala del punto del

terreno di sinistra è stata costruita tenendo presente l'angolo di inclinazione e

l'altezza media degli occhi di 1,6 m/5,5 piedi.

ALLOGGIAMENTO PER LO STRUMENTO SUUNTO KB-14 E PM-5

L'alloggiamento dello strumento è adatto per i seguenti modelli KB e PM:

KB-14 (tutti i modelli) e PM-5.

La pagina si sta caricando...

Suunto PM-5 Manuale utente

Questo manuale è adatto anche per

Suunto PM-5 Manuale utente

in altre lingue

Documenti correlati

Altri documenti